#ucore-lab2
大概就是记录一下lab2这些东西，前面的代码基本上是阅读得到的结果，主要写写自己怎么实现的伙伴系统就完了（

ex1

首先需要掌握关于ucore里边双向链表的东西，这里直接贴实验指导书的内容，这一部分就是关于ucore的数据结构的知识。这个空闲块链表实际上是将各个块首页的指针集合（由prev和next构成）的指针（或者说指针集合所在地址）相连。这块需要看懂。说实话这玩意挺巧的。。。

然后就可以看本次实验了。ex1很水，就改几行，但是自己要懂原理。也就这个能自己写出来

ex2 ex3

一个比一个恶心了。得先看书，把内存管理那块看懂，不然绝对看裂开。其实明白了内存管理，然后再看注释，可能自己也差不多能写出来了，但是考虑到要自己调试，基本上要裂开一定的过程，就算了，阅读代码即可。

ch1

写在前面

伙伴系统，一个被人实现了快烂了的东西。大概有三种数据结构可以写这个东西，分别是队列数组、树状数组和线段树。我采用线段树实现。当然，由于伙伴系统的优美特性，是满二叉树的结构，那么其实可以采用zkw线段树实现，代码更少更优美。据网络上说随着zkw线段树的普及，基本上没人用树状数组了，树状数组这玩意不会也行。

网上教程很多，采用链表（队列数组）被认为是最接近操作系统实现的。但是你一看这个结构，肯定率先想线段树（zkw线段树），因此这样写虽然性能不一定最优，但一定非常自然。

然后在我况吃况吃写了两天之后，我实现的破玩意越来越丑但思想越来越像zkw线段树，虽然能跑了但始终有地方不太优美，被迫去学了一下zkw线段树。后来发现也有人这么实现过，是个清华的佬，因此参考了一些他的代码。其实一开始用普通的线段树的思想已经实现了，但是测试一直有一些案例过不去，也不知道为什么我编样本的能力这么强。。。最后改来改去就开始逼近zkw线段树了**（这个过程略草，非常难蚌，在此处不宜展开，尤其不能说我经历了什么以及最后我是怎么知道这玩意是zkw线段树的。只能说没有金刚钻别揽瓷器活，在没研究过算法的情况下我建议先刷刷洛谷、乐扣、牛客。）**最后，由于代码经过多次迭代，部分内容仍有不可更改、不可解释的现象，请自行查找资料进行优化。。。

下面先介绍线段树和zkw线段树，已经会的和不感兴趣的可以直接跳过看最后的代码。

线段树

首先，我们要介绍一下线段树这种书上没写、课上没讲但是很牛很有用的数据结构。跪谢松子桂鱼大佬花了俩小时给我讲这个玩意。这里的部分讲解和图片参考了这个博客

首先什么是线段树

线段树是一种二叉搜索树，什么叫做二叉搜索树，首先满足二叉树，每个结点度小于等于二，即每个结点最多有两颗子树，何为搜索，我们要知道，线段树的每个结点都存储了一个区间，也可以理解成一个线段，而搜索，就是在这些线段上进行搜索操作得到你想要的答案。

线段树能够解决什么样的问题

这里不展开具体内容，只是说线段树的适用范围很广，线段树由于本身是专门用来处理区间问题的，可以在线维护修改以及查询区间上的最值，求和。线段树的每一个节点都储存着一段区间$[L,R]$的信息。它的大致思想是：将一段大区间平均地划分成2个小区间，每一个小区间都再平均分成2个更小区间……以此类推，直到每一个区间的$L$等于$R$（这样这个区间仅包含一个节点的信息，无法被划分）。通过对这些区间进行修改、查询，来实现对大区间的修改、查询。以P3372模板题为例，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
如题，已知一个数列，你需要进行下面两种操作：

将某区间每一个数加上 kk。
求出某区间每一个数的和。

输入格式
第一行包含两个整数 n, mn,m，分别表示该数列数字的个数和操作的总个数。

第二行包含 nn 个用空格分隔的整数，其中第 ii 个数字表示数列第 ii 项的初始值。

接下来 mm 行每行包含 33 或 44 个整数，表示一个操作，具体如下：

1 x y k：将区间 [x, y][x,y] 内每个数加上 kk。
2 x y：输出区间 [x, y][x,y] 内每个数的和。
输出格式
输出包含若干行整数，即为所有操作 2 的结果。

输入
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

输出
11
8
20

如上所示，是一个数列$[1,5,4,2,3]$，我们希望对其中某一端数字进行区间操作，比如对下标1到5即$a[0],a[4]$都加上1，然后查询区间$a[1]+a[2]+a[3]+a[4]$的和。

这就是区间加法，即对于一个区间$[L,R]$上的问题，可以通过$[L,M]$和$[M+1,R]$的分别处理来实现。可以看出线段树就是分块思想的树化，类似于算法导论里扔瓶子的问题，使原来使用for循环遍历的$O(N)$的复杂度下降到$O(logN)$这个级别。

首先说一个节点都有什么（其实除了区间，想加什么就加什么）

1
2
3
4
5
struct node{
    long long int l,r;//l,r代表区间[l,r]
    long long int sum;//是区间和，如果是叶子节点，就是那个数列里这个位置的数值
    long long int flag;//据说叫懒惰标记，很深，很巧，用处很大
};

下面讲一下建树的过程

1
2
3
4
5
6
7
8
9
void build(ll i,ll l,ll r)
{
  if(l==r){list[i]=a[l];return ;}//如果左右区间相同，那么必然是叶子节点，只有叶子节点是被真实赋值的
  ll mid=(l+r)>>1;
  build(ls(p),l,mid);
  build(rs(p),mid+1,r);
//此处由于我们采用的是二叉树，所以对于整个结构来说，可以用二分来降低复杂度，否则树形结构则没有什么明显的优化
//啥意思也没太懂，反正网上这么写我也这么解释
}

这里关于这个位运算要解释一下是怎么回事，其实就是一个加快的操作。先看图1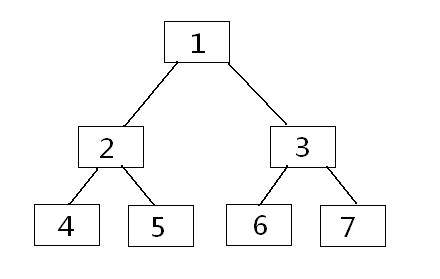图1
可以发现每个节点的左儿子都是父节点的二倍，右儿子是二倍加一再看图2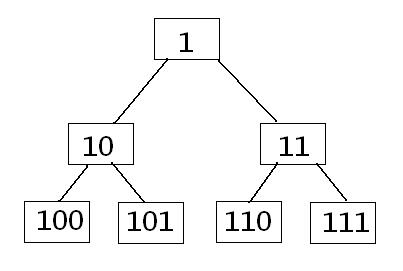图2
然后他们在二进制下长这样。二倍就直接左移，二倍加一就左移再和1逻辑或，由于左移完了末位是0，相当于加一了。为啥不直接加一呢，因为汇编告诉我们都用逻辑运算会非常快，本人亲测快一倍的样子。

1
2
3
4
5
6
7
8
9
void build(ll i,ll l,ll r)
  if(l==r){list[i]=mynode[i];return ;}//如果左右区间相同，那么必然是叶子节点，只有叶子节点是被真实赋值的
  ll mid=(l+r)>>1;
  build(i,l,mid);
  build(i,mid+1,r);
  mynode[i].sum=mynode[i<<1].sum+mynode[i<<1|1].sum;//此处应该有个update()函数，不过我没写，哈哈
//此处由于我们采用的是二叉树，所以对于整个结构来说，可以用二分来降低复杂度，否则树形结构则没有什么明显的优化
//啥意思也没太懂，反正网上这么写我也这么解释
}

下面是pushdown操作，用于区间更新的，等于我不给每个节点都更新，等用到了我再往下传。本次实验用处不大，过些日子我总结算法重新写这些东西再解释。

1
2
3
4
5
6
7
8
9
10
11
12
void pushdown(int i){
    if(mynode[i].flag==0){
        return;
    }
    else{
        mynode[2*i].sum+=mynode[i].flag*(mynode[2*i].r-mynode[2*i].l+1);
        mynode[2*i+1].sum+=mynode[i].flag*(mynode[2*i+1].r-mynode[2*i+1].l+1);
        mynode[2*i].flag+=mynode[i].flag;
        mynode[2*i+1].flag+=mynode[i].flag;
        mynode[i].flag=0;
    }
}

然后区间修改。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void add(int j,int lef,int rig,int i){
    if(lef<=mynode[i].l&&mynode[i].r<=rig){
        mynode[i].flag+=j;
        mynode[i].sum+=j*(mynode[i].r-mynode[i].l+1);
        return;
    }
    else if(lef>mynode[i].r||rig<mynode[i].l){
        return;
    }
    else{
        pushdown(i);
        add(j,lef,rig,2*i);
        add(j,lef,rig,2*i+1);
        mynode[i].sum=mynode[2*i].sum+mynode[2*i+1].sum;
    }
}

最后查询

1
2
3
4
5
6
7
8
9
10
11
12
13
void ask(int lef,int rig, int i){
    if(lef<=mynode[i].l&&mynode[i].r<=rig){
        ac+=mynode[i].sum;
    }
    else if((lef>mynode[i].r)||(rig<mynode[i].l)){
        return;
    }
    else{
        pushdown(i);
        ask(lef,rig,2*i);
        ask(lef,rig,2*i+1);
    }
}

就完事了。当然这玩意还有各种骚操作，有兴趣可以看这篇博客。

然后介绍本次实验的重头戏——zkw线段树

由大神zkw自己提出来的数据结构。zkw线段树的结构是一个满二叉树的形式。可以定义$M$表示最后一层的叶节点数，显然$M≥n$ ，非叶节点有$M−1$个。但是我们在区间修改时，需要多2个节点$0$和$n+1$（好像有人证明n+1是没有必要的，经过我自己简单实验确实是这样），因此$M≥n+1$，那么第 i 个叶节点编号就为M+i。而且好处就是代码量特别短，一个功能一行就能实现。接下来全文照搬blog。

查询区间[1,n]，先建树

1
2
3
4
5
int n,M,q;int d[N<<1];
inline void Build(int n){
    for(M=1;M<n;M<<=1);
    for(int i=M+1;i<=M+n;i++) d[i]=in();
}

维护区间和

1
for(int i=M-1;i;--i) d[i]=d[i<<1]+d[i<<1|1];

维护最大值

1
for(int i=M-1;i;--i) d[i]=max(d[i<<1],d[i<<1|1]);

维护最小值

1
for(int i=M-1;i;--i) d[i]=min(d[i<<1],d[i<<1|1]);

然后是单点操作单点修改

1
2
3
void Change(int x,int v){
    d[M+x]+=v;
}

只是这么简单？当然不是，跟线段树一样，我们要更新它的父节点！

1
2
3
4
void Change(int x,int v){
    d[x=M+x]+=v;
    while(x) d[x>>=1]=d[x<<1]+d[x<<1|1];
}

没了？没了。

单点查询(差分思想，后面会用到)
把d维护的值修改一下，变成维护它与父节点的差值建树的过程就要修改一下咯！

1
2
3
4
void Build(int n){
    for(M=1;M<=n+1;M<<=1);for(int i=M+1;i<=M+n;i++) d[i]=in();
    for(int i=M-1;i;--i) d[i]=min(d[i<<1],d[i<<1|1]),d[i<<1]-=d[i],d[i<<1|1]-=d[i];
}

在当前情况下的查询

1
2
3
void Sum(int x,int res=0){
    while(x) res+=d[x],x>>=1;return res;
}

区间那块不太需要了。此处不写了。

代码实现

代码本身没啥可说的其实，有几点要注意。在明白了zkw线段树的建树过程之后，我们知道，我们会申请一个数组去存放需要存的页。注意，这里我们需要先探测一下有多少内存空间再申请数组，一上来duang一下申请一个固定的数组而且还是1w肯定是不对的（比如某位学长的，16384个页他只申请了10000长度的区间，逗我呢。天问之路那个猛人和清华17级的一个人写的是对的）

释放的维护我抄了一下，不然自己写的话，要写很多行。其他的不需要，尤其是pushdown操作。当我们要分配某一个节点的时候，把他变成零就好，因为遍历的时候到零就停了，他的子孙节点并不需要被更新。一开始还写了这破玩意，导致后面维护几乎不可能，极其难蚌。

整体代码不难，因为zkw线段树本身就是非常优美的数据结构，而且本身代码量就短。

然后我再写一点分析大佬的代码。

1
buddy_page = (unsigned int*)KADDR(page2pa(base));

这一行背后的内容很多。他利用了物理页在内存空间中是通过一维数组管理的这个特性。首先，由于初始时内存空间是连续的，那么将基址转化成物理地址，这一步实际上自动把所有页连接好通过一维数组管理了，这就是为什么他的init函数不写任何内容的原因。然后转化成内核地址。这样就靠物理页的数组来管理zkw线段树了。不过他这样是不是有点危险？我也搞不太懂，等我过两天写完os近期的knowledge总结再说。其实后面还有一段就是他说保留了33个页给伙伴系统，这一点我认为应该是由ucore自动完成的，不应该是自己写的，不知道我理解的正不正确。不过我没按照他这么做，一样能通过，所以，暂时假设我说的是对的。